前言

对java的Math.random()函数分析，从而初识对数器的概念。

热身

题目

有这么一个需求，对一个整形数组a位置到b位置求和，并且需求量很大，一秒几万次的那种，这么时候明显，单纯的循环运算方法已经没法满足这么多次的请求，性能太差了。所以，我们可以算出来啊，直接取数据就完事了啊，很抽象？举例！

解决思路

假设，有一个数组是

1
[1 6 -1 9 7 8]

我们抽象出一个正方形，他有x y 轴 ，并且x y 轴的数据对应的是这个数组数据，我么你只需要以y轴主，填数据是x y轴相加的值即可，直接抽象

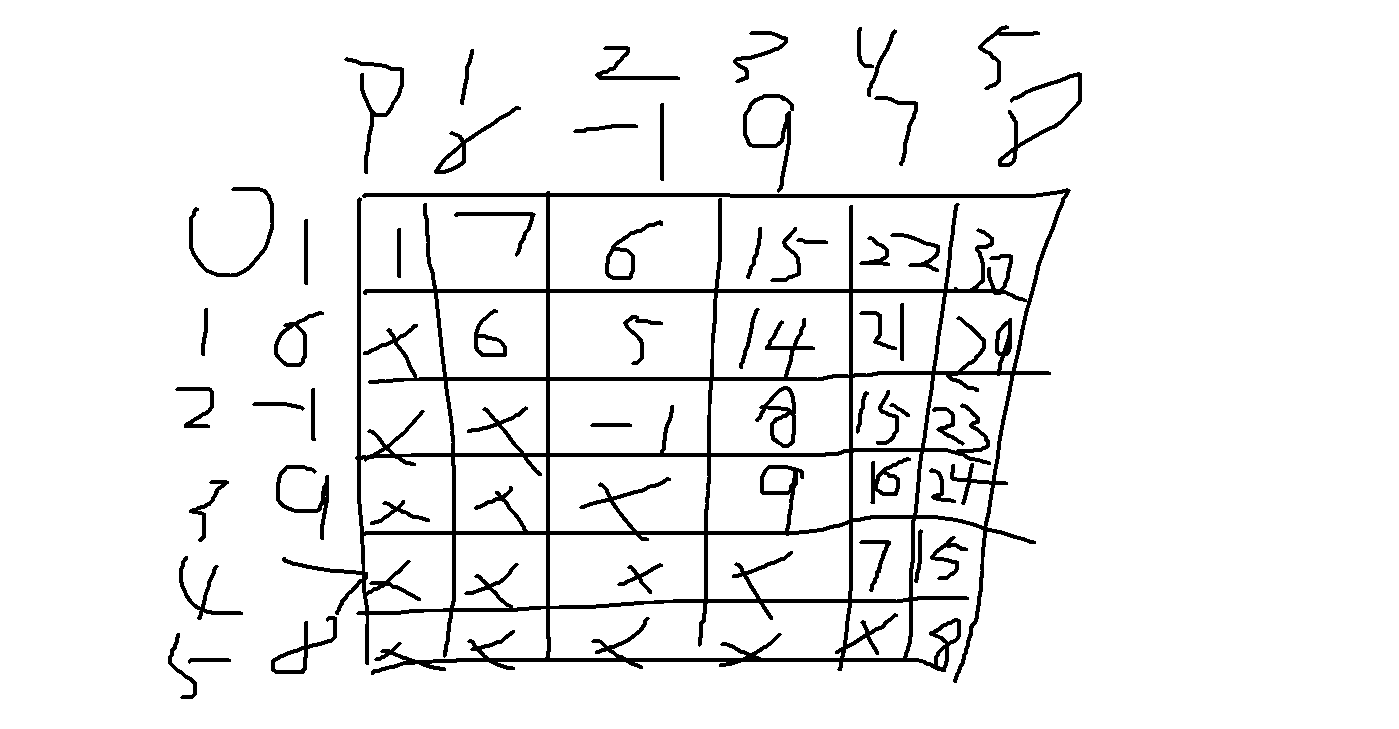
image-20220106205824448

看上图，是有点抽象。。。但是大致意思写出来了。直接解释就是，外面的是数组角标，里面是对应的值，我们逻辑走一遍。

0->0=1,0->1=7,0->2=6….0->5=30

1->0不存在，1->1=6…1->5=29

…

下面我就不写了很好理解，就等于把所有可能性都算出来，存下来，如果要用直接取就行。

那么，怎么去实现了，其实很好理解，这个玩意就是二维数据，我们直接写代码，看如何加载的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public static int[] arr = new int[]{1, 6, -1, 9, 7, 8};
public static int[][] arrStartToEndSum = new int[arr.length][arr.length];

static {
    //加载数组
    for (int i = 0; i < arr.length; i++) {
        for (int j = 0; j < arr.length; j++) {
            //如果开始角标大于结束角标就跳过
            if (j < i) {
                continue;
            }
            //如果开始等于结束角标，直接取值
            if (i == j) {
                arrStartToEndSum[i][j] = arr[j];
            } else {
                //否则就是前面加后面的
                arrStartToEndSum[i][j] = arrStartToEndSum[i][j - 1] + arr[j];
            }
        }
    }
}

简单解释一下：

第一个for循环代表是开始的角标，第二个循环代表是结束的角标，而开始的角标是不能大于结束的角标的，所以这里跳过。

如果开始角标和结束角标是相等的，那么就是这个数组的本身。如果不是，那就是需要二维数组的第二个数据用前面数字加当前结束角标对应的值。

很简单，使用起来也很简单，直接写一个方法，直接调用即可。

1
2
3
4
5
6
7
8
9
10
public static int queryArraysStartToEndSum(int startIndex, int endIndex) {
    //这里就直接取就行了
    if (startIndex > endIndex) {
        return -1;
    }
    if (startIndex > arr.length || endIndex>arr.length) {
        return -1;
    }
    return arrStartToEndSum[startIndex][endIndex];
}

优化算法思路

没错这还可以优化，我不想整什么二维数据，太麻烦了，想直接一维数组整出来，可以吗？可以！！！这个就是这道题的秒解了：前缀和

还是数组举例

1
[1 6 -1 9 7 8]

我们新建一个数据，和原数组同样长度，只不过，每个位置的数据是前面相加的数据，然后套公式arr[endIndex]-arr[startIndex-1]，即可得到我们想要数据

1
[1 7 6 15 22 30]

懂没懂，理解没理解？没关系举例！

我想取1->2位置的数据，6-1=5

我想取2->5位置数据，30-7 = 23

…

有点感觉没？理解没？不理解没关系，我们套字母

原数组

1
[a,b,c,d,f,d]

前缀和数组

1
[a,a+b,a+b+c,a+b+c+d,+a+b+c+d+f]

我想取1->2位置的数据，a+b+c-a=b+c

我想取2->5位置数据，a+b+c+d+f-a+b=c+d+f

…

是不是很好理解！！！

直接上代码

1
2
3
4
5
6
7
8
9
10
11
public static int[] arr = new int[]{1, 6, -1, 9, 7, 8};
public static int[][] arrStartToEndSum = new int[arr.length][arr.length];
public static int[] preSumArr = new int[arr.length];

static {
    //加载数组
    preSumArr[0] = arr[0];
    for (int i = 1; i < arr.length; i++) {
        preSumArr[i] = arr[i] + preSumArr[i - 1];
    }
}

取的逻辑就很简单了，套公式即可，注意特殊的条件即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public static int queryArraysStartToEndSum2(int startIndex, int endIndex) {
    //这里就直接取就行了
    if (startIndex > endIndex) {
        return -1;
    }
    if (startIndex > arr.length || endIndex>arr.length) {
        return -1;
    }
    //如果开始角标等于0，直接返回
    if (startIndex==0) {
        return preSumArr[endIndex];
    }

    return preSumArr[endIndex]-preSumArr[startIndex-1];
}

等概率函数分析

Math.random()函数，是随机获取一个double类型的数值，并且是等概率的，啥玩意，直接出结论？你总该去论证啊！那我们开始论证。那么怎么去论证呢？随机100000次，随机获取0.3以下的数值是比例是多少？代码很简单

1
2
3
4
5
6
7
8
9
10
11
int times = 100000;
int count = 0;

/* 正常循环判断是否是等概率 */
for (int i = 0; i < times; i++) {
    double random = Math.random();
    if (random < 0.3) {
        count++;
    }
}
System.out.println("正常测试Math.random()概率为+" + ((double) count / (double) times));

结果：

image-20220106215833783

发现，唉差不过啊，那我们试试0.8以下的数值出现的比例

image-20220106215935155

唉呀。还是差不多，我不信这个邪了，我们看0.17以下数值出现的比例

image-20220106220030976

还是差不多，那已经能论证Math.random()是一个等概率函数。

那他有什么用？？？我就算知道他是等概率的函数，又能干什么呢？当然能干很多事了，这么牛逼的函数我们只会用两个字来形容：赌怪！！！

？？？赌怪？？？单走一个6！！！

嗯哼，串台了，是转化，没错转化，既然我知道，这个赌怪函数获取数值是随机的，那我对这个等概率的数值，转化成某个数值，他也是等概率出现的，你可以理解成一个映射，一个等概率的数值可以转化成另一个等概率数值。直接来个算法题理解下

概率算法题一

题目

写一个获取0-5等概率的函数

思路

可以利用Math.random()函数的等概率函数特性，获取一个等概率数值，然后乘以6，并转成整形，那么得到的整形也是等概率的！

解

直接上代码

1
2
3
public static int f01() {
    return (int) (Math.random() * 6);
}

没错就是这么简单粗暴，代码有了，直接代码验证

1
2
3
4
5
6
7
8
9
10
11
System.out.println("=============================");
/* 想要0~6等概率函数*/
int[] counts = new int[6];
count = 0;
/* 正常循环判断是否是等概率 */
for (int i = 0; i < times; i++) {
    counts[f01()]++;
}
for (int i = 0; i < counts.length; i++) {
    System.out.println("index->" + i + "，value->" + counts[i]);
}

结果：

image-20220106222134571

发现不管执行多想次，0-5的次数都是差不多的，好了，我们写完了，写了一个0-5等概率函数。就这一个玩法？不还有！

概率算法题二

题目

输入一个x，值范围是[0-1)，获取的数值的概率是x的平方，写一个函数

思路

既然是平方，那我只有一个等概率的函数，怎么整成平方的概率呢，还有是x的平方。。。哎，那我执行两次赌怪方法，不就代表，获取一个x的概率是平方吗，就是x * x，那我执行两次，取哪个值呢？取最大的！这是什么说法？

第一次取的值是x以下的概率是x，第二次取的值是x以下的概率同样是x，必须满足两次取值都是x以下，才满足概率是x的平方。那么，怎么去保证两次取值都是x平方以下的值呢？只需要取最大值是x值以下的就行，理解没？

为什么不能取最小值？我们反着思考，我们的条件是取的值还是x以下，那么取不到x值以下的概率值是什么？如果取最小的，只需要执行两次赌怪函数的值任意一次是x以下的值就行了，但是这样不好理解，不好套公式，于是，我么反着来，两次取不到x函数以下的概率是多少？

(1-x)(1-x)，为啥是这个，自己看上面取x的概率逻辑，从而推断出，满足取出x以下数值的概率是1-(1-x)(1-x)，这样明显不满足题了，我们要的是x平方的概率。废话，不多说，直接上代码

解

1
2
3
public static double f02() {
    return Math.max(Math.random(), Math.random());
}

没错，bb一大堆，代码就是这么简单，那么来验证啊，直接上验证代码

1
2
3
4
5
6
7
8
9
10
System.out.println("=============================");
/*调整0~x出现概率为x的平方*/
double x = 0.35;
count = 0;
for (int i = 0; i < times; i++) {
    if (f02() < x) {
        count++;
    }
}
System.out.println(String.format("x值：%s，x平方：%s，f02()函数获取x值以下数值的概率是：%s",x, Math.pow(x, 2), (double) count / (double) times));

结果：

image-20220106224636578

没错，我们又给这玩意整出来了，继续！！！

概率算法题三

题目

接算法题一，已知f01函数是获取0-5的整数等概率函数，写一个获取1-7整数等概率函数

思路

乍一看，很难，其实很难，但是我们知道转化，那么怎么转化呢，乘以某个数值转吗？？？似乎好像不行，有个1怎么乘啊，0乘以任何数都是0，这个0始终是存在的，我们的题目是1开始。

既然，这样，我们能不能把他转化为某种形式，从而转成为任何值呢？有！二进制！！！没错，二进制组成的是0和1，那我写一个函数，就是取0和1等概率，不就代表我二进制转化成的值都是等概率的！

再去分析f01函数，是0-5的等概率，那么我的逻辑是取的值，0-2返回0,3-5就返回1，哎，那这样是不是想要取0和1，对应的函数必须是偶数个？不然，不好分概率的啊，非也，如果等概率函数函数获取值是中间数，重新取一次即可。

那么，有了获取0 1 等概率函数，只剩下转化，怎么转化呢？位运算想加呗，看题目是要1-7等概率，我们需要3位二进制，等于说0 1等概率函数执行三次即可

解

直接上代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public static int f03() {
    return f01() < 3 ? 0 : 1;
}

public static int f04() {
    int ans = 0;
    do {
        int ans1 = f03() << 2;
        int ans2 = f03() << 1;
        int ans3 = f03() << 0;
        ans = ans1 + ans2 + ans3;
        //这里只需要1-7的值，如果最终的结果是0，那就重新获取
    } while (ans == 0);
    return ans;
}

直接上验证代码

1
2
3
4
5
6
7
8
System.out.println("=============================");
counts = new int[8];
for (int i = 0; i < times; i++) {
    counts[f04()]++;
}
for (int i = 0; i < counts.length; i++) {
    System.out.println("index->" + i + "，value->" + counts[i]);
}

结果：

image-20220106231153425

看结果，我们又整出来了，这里注意的点是，如果二进制转化的值，不是想要的，就重新执行即可，你可以理解给概率分到符合条件的数值上去。

概率算法题四

题目

有一个固定概率黑盒函数，返回数值0和1，我们不知道概率是多少，但是概率是固定的，写一个等概率1-7的函数

思路

其实，还是转化，还是转成等概率0和1，只不过，因为他是固定概率，所以，我们可以取两次，如果是不同的值，就代表这次的概率是固定的，然后我们设定规则，如果第一个取的值是0，第二次取的值是1，就返回0。如果第一次取的值是1，第二次取的值是0，那么返回1。其他情况重新执行。

解

直接代码，只写函数，其他不写了

1
2
3
4
5
6
7
8
9
10
11
12
//固定概率函数
public static int f05() {
    return Math.random() < 0.3 ? 0 : 1;
}

public static int f06() {
    int ans = 0;
    do {
        ans = f05();
    } while (ans == f05());
    return ans;
}

结尾

打完收工！！！